Advanced-Single Chains

Single's Chains (a.k.a Colouring, Open Chain of Sudo)
Chains form a big part of the advanced strategy armory. Fortunately there is a very simple chain of clues thats works with single candidate numbers only. We can scan the board for a configuration looking at one number at a time.

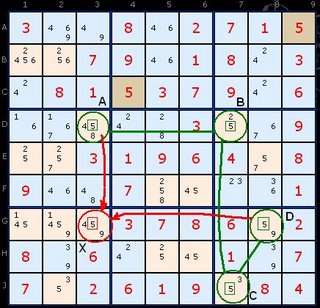
Let N be our candiate we're scanning the board for. We are looking for pairs of N in any row, column or box. Having three or more won't do and we must ignore units with more than two of N. If we can join a sequence of these pairs we'll form a chain. Obviously the corners of this chain must change from one type of unit to another - for example a pair in a row followed by a pair in a column and then a row again or a box. In the example to the right there are only two 5's at A and B IN THAT ROW. Our first pair. B and C link two 5's in their column. And so on to D
We are hoping to make an odd number of links (the green lines in the diagram). If we do then something very useful occurs.

[Home] - [Personal] - [Sudoku Solver] - Advanced Strategies
Goto Basic Strategies Naked Pairs Naked Triples Naked Quads Hidden Pairs Hidden Triples Hidden Quads Intersection Removal Goto Fishy Strategies X-Wing Sword-Fish Jelly-Fish Multivalue-X-Wing Finned X-Wing Sashimi Finned X-Wing Advanced Strategies on this page Singles Chains a.k.a Simple Colouring Multi-Colouring Y-Wing a.k.a XY-Wing Y-Wing Chain XY-Chains XYZ-Wing WXYZ-Wing Aligned Pair Exclusion Remote Pairs Unique Rectangles Guardian/Broken Wings Death Blossom
Single's Chains (a.k.a Colouring, Open Chain of Sudo)
Chains form a big part of the advanced strategy armory. Fortunately there is a very simple chain of clues thats works with single candidate numbers only. We can scan the board for a configuration looking at one number at a time.

Let N be our candiate we're scanning the board for. We are looking for pairs of N in any row, column or box. Having three or more won't do and we must ignore units with more than two of N. If we can join a sequence of these pairs we'll form a chain. Obviously the corners of this chain must change from one type of unit to another - for example a pair in a row followed by a pair in a column and then a row again or a box. In the example to the right there are only two 5's at A and B IN THAT ROW. Our first pair. B and C link two 5's in their column. And so on to D
We are hoping to make an odd number of links (the green lines in the diagram). If we do then something very useful occurs. Singles Chain Example 1: Load Example or From the start
Pretend for one moment that A is 5. B cannot be which forces C to be 5 which eliminates 5 from D.Now think in reverse.If D is 5 then C cannot be, B must be and A cannot be. Whatever way round you think it through EITHER A OR D must be a 5. Any cell that both A and D can see cannot contain a five - in this case D8 and G3. Since there is a 5 at G3 (marked with X) we can removed it. Have a look at the next strategy for an explanation for cells 'seeing' each other.
As long as the chains are linked by an ODD number of links and there is only two candidates in each unit of each link, this strategy will work. We can describe the two options in this way (~ means NOT 5):
A(5) -> B(~5) -> C(5) -> D(~5) = X(~5)ORA(~5) -> B(5) -> C(~5) -> D(5) = X(~5)

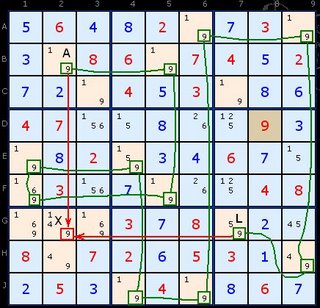
Chains can be any length. In some cases, ridiculously long as in this example. Here twelve cells (A to L) are joined by eleven links to target the cell at G2. The minimum number of links is 3. It will be a rare occasion if you need more than 5.


Another way of looking at this is the popular technique of Colouring. We'll go back to our first example. You assign the start of a promising chain with an arbitary colour, in this case Green (A at D3). Remember, we are only looking at candidate 5 and units with two 5s in them (called conjugate pairs).
A has two conjugate pairs, B and X - which are painted in an alternative colour, blue. From cell B I can find two more pairs at C and E which I colour in green. Both these point to D which must be coloured blue, as well as F along the bottom row.
Now we have arrived at the contradiction. X and D are both blue and they are in the same unit (the row in this case).
Our first rule is: whenever a candidate outside the chain relates by column, row or box to two alternately coloured cells in a singles chain, that 'non-chain' candidate can be excluded. This applies to X.
But not only can we trace a chain from A to D which eliminates the 5 at X but we can say something more general and much more interesting. Either ALL the green cells are 5 or ALL the blue cells are 5. Because we have two blue cells in the same row blue must be false. Green must contain ALL the 5s. That gets us a huge number of cells solved in one go.
Our second rule is: Whenever two cells in a singles chain have the same colour and also share the same unit, that color must be the 'false' color since each unit can only have one of any candidate value.