1:A Pair or Triple in a box - if they are aligned on a row, n can be removed from the rest of the row. 2:A Pair or Triple in a box - if they are aligned on a column, n can be removed from the rest of the column. 3:A Pair or Triple on a row - if they are all in the same box, n can be removed from the rest of the box. 4:A Pair or Triple on a column - if they are all in the same box, n can be removed from the rest of the box.
Rules 1 and 2 are also called Pointing Pairs/Triples Rules 3 and 4 are also called Box/Line Reduction
Type 1 - Pointing Pairs/Triples Strategy (a.k.a. Intersection Removal) Looking at each box in turn there may be two or three occurrences of a particular number.If these numbers are aligned on a single row or column (as a pair or a triple) then we know that number MUST occur on that line. Therefore, if the number occurs anywhere else on the row or column outside the box WHICH THEY ARE ALIGNED ON then it can be removed. The pair or triple points along the line at any numbers which can be removed.
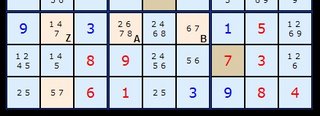
Consider the lower third of the puzzle board above. We are looking at the number 7 in the center box. It can only be found in the top row at A and B. The 7 at Z in the left hand box can be removed. Following on from this discovery it means the 7 in the last row must be in column 2 (where it currently says 5/7).
Type 2 - Box Line Reduction Strategy (a.k.a. Intersection Removal) This strategy involves careful comparison of rows and columns against the content of boxes (3 x 3 squares). If we find numbers in any row or column that are grouped together in just one box, we can exclude those numbers from the rest of the box. For example:
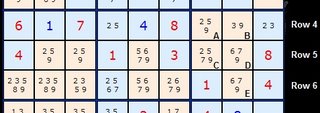
Consider the right hand box in this center row of the board. We can see five squares with 9s marked as possible numbers. The 9s that exist in cells A and B are the only 9s in that whole row. Either A or B MUST contains a 9 in the final solution. We can therefore safely remove the 9s from C, D and E.
Credits
No comments:
Post a Comment