Advanced-XY Chains

XY-Chains
The Y-Wing Chains are infact part of a more encompassing strategy called XY-Chains. The commonality is the same pincer-like attack on candidates that both ends can see and that the chain is made of bi-value cells. With Y-Chains the hinge was expanded to a chain of identical bi-value cells but in an XY-Chain these can be different - as long as there is one candidate to make all the links. The "X" and the "Y" in the name represent these two values in each chain link. The example here is a very simple XY-Chain of length 4 which removed all 5's in the pink cells. The chain ends are A7 and C2 - so all cells that can see both of these are under fire. It's possible to start at either end but lets follow the example from A7. We can reason as follows
1: If A7 is 5 then A3/C7/C9 cannot be. 2: if A7 is NOT 5 then it's 9, so A5 must be 2, which forces A1 to be 6. If A1 is 6 then C2 is 5.Which ever way round A7 is the 5's in A3/C7/C9 cannot be 5. The same logic can be traced from C3 to A7 so the strategy is bi-directional, in the jargon.

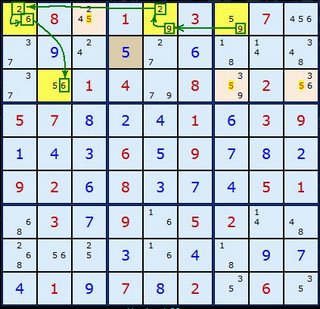
Here is a much longer seemingly more complex XY-Chain of length 10 - attacking 6's in the pink cells. I've shaded the two chain ends in green. I've also left the arrow head's off so you can trace the XY-Chain from either end. Doing so you'll quickly release that 6 must be at one end or the other, so there is no chance of other 6's which both ends can see.

When you've got a good spread of bi-values this is a useful trick. Remote Pairs, described below are also a special sub-set of XY-Chains - they merely have a double-chain of inference through both values in each chain link because they contain the same values from start to end. Remote Pairs were discovered/described first before this more general approach.