This is an extension of Y-Wing or (XY-Wing). John MacLeod defines one as three cells that contain only 3 different numbers between them, but which fall outside the confines of one row/column/box, with one of the cells (the 'apex' or 'hinge') being able to see the other two; those other two having only one number in common; and the apex having all three numbers as candidates. It follows therefore that one or other of the three cells must contain the common number; and hence any extraneous cell (there can only be two of them!) that "sees" all three cells of the Extended Trio cannot have that number as its true value.

It gets its name from the three numbers X, Y and Z that are required in the hinge. The outer cells in the formation will be XZ and YZ, Z being the common number.

In this example the candidate number is 7 and R3C5 is the Hinge. It can see a 1/7 in R2C4 and a 5/7 in R3C8. We can reason this way: If R2C4 contains a 1 then R3C5 and R3C8 become a naked pair of 5/7 - and the naked pair rule applies. Same with R3C8. If that's a 5 then R2C4 and R3C5 become a naked pair of 1/7 each. If any of the three are 7 then 7 is still part of the formation. Any 7 visible to all three cells must be removed, in this case in R3C6.
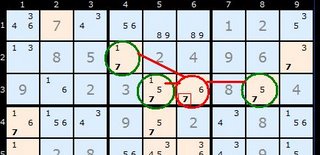
The second example shows a double XYZ-Wing. R4C6 is common to both XYZ-Wings.
No comments:
Post a Comment