This is an excellent candidate eliminator. The name derives from the fact that it looks like an X-Wing - but with three corners, not four. The forth corner is where the candidate can be removed but it leads us to much more as we'll see in a minute. Lets look at Figure 1 for the theory.

A, B and C are three different candidate numbers in a rectangular formation. In two corners an occurrence of A is shared with another number C. B also shares C. The cell marked AB is the key. If the solution to that cell turns out to be A then C will definitely occur in the lower left corner. If AB turns out to be B then C is certain to occur in the top right corner. C is a complementary pair.
So whatever happens, C is certain in one of those two cells marked C. The red C is can be 'seen' by both Cs - the cell is a confluence of both BC and AC. Its impossible for a C to live there and it can be removed.
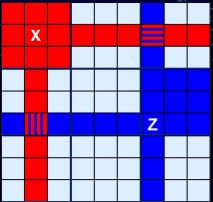
In Figure 2 I'm demonstrating the sphere of influence two example cells have, marked red and blue. X can 'see' all the red cells, Z can 'see' all the blue ones. In this case there are two cells which overlap and these are 'seen' by both.

If our A, B and C are aligned more closely they can 'see' a great deal more cells than just the corner of the rectangle they make. In Figure 3 BC can see AB because they share the same box. AC can see AB because they share the same row. BC and AC can see all the cells marked with a red C where this Y-Wing can eliminate whatever number C is.

In this first example we have lots of 1s, 2s and 3s, but three cells - marked in green rings - form a Y-Wing. The two 2s on the end form the pincer - one of them must be a 2. Therefore the 2 marked in a red box can be eliminated.

The second example in Figure 5 shows three candidate 8s being eliminated from a single Y-Wing. The Y-Wing consists of 1/8, 1/5 and 5/8.
No comments:
Post a Comment