Unique Rectangles takes advantage of the fact that published Sudokus have only one solution. If your Sudoku source does not guarantee this then this strategy will not work. But it is very powerful and there are quite a few interesting variants.
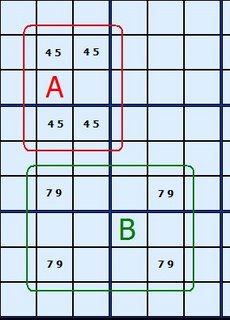
Noticing the 'Deadly Pattern'
In Figure 1 we have two example rectangles formed by four cells each. The pattern in red marked A consists of four conjugate pairs of 4/5. They reside on two rows, two columns and two blocks. Such a group of four pairs is impossible in a Sudoku with one solution. The reason? Pick any cell with 4/5. If the cell solution was 4 then we quickly know what the other three cells are. But it would be equally possible to have 5 in that cell and the others would be the reverse. There are two solutions to any Sudoku with this deadly pattern. If you have achieved this state in your solution something has gone wrong. The pattern ringed in green looks like a deadly pattern but there is a crucial difference. The 7/9 still resides on two rows and two columns, but instead if two boxes it is spread over four boxes. Now, such a situation is fine since you can't guarantee that swapping the 7 and 9 in an alternate manner will produce two valid Sudokus. One of them is the real solution, the other a mess. Why? Swapping the 7 and 9 around places them in different boxes and 1 to 9 must exist in each box only once. In the red example, swapping within the box does not change the content of that box.
Type 1 Unique Rectangles
 Figure 1
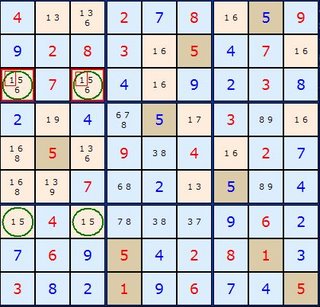
Figure 1For all Unique Rectangles we are going to look for potential deadly patterns and take advantage of them. A Type 1 Unique Rectangle is illustrated in Figure 2. The three circles marked in green rings contain 5/7. The fourth corner marked with a red square also contains 5/7 and two other candidates. If the 3/6 were removed from that cell we would have a Deadly Pattern. This cannot be allowed to happen so its safe to remove 5 and 7 from that cell. The proof is pretty straightforward once you get your head around the basic idea. Assume R5C6 is 5. That forces R5C4 to be 7, R2C6 to be 7, and R2C4 to be 5. That's the deadly pattern; you can swap the 5's and 7's and the puzzle still can be filled in. So if the Sudoku is valid, R5C6 cannot be 5. The exact same logic applies if you assume R5C6 is 7. So R5C6 can't be a 5, and can't be a 7 - it must be either 3 or 6.
Type 2 Unique Rectangles
In Figure 3 we have a similar pattern, but this time, R2C4 and R2C6 (green circles at the top), the squares which share the same block have a single extra possibility - in this case, 8. To make subsequent discussion easier to follow, we will refer to the two squares that only have two possibilities as the floor squares (because they form the foundation of the Unique Rectangle); the other two squares, with extra possibilities shall be called the roof squares.

In this "Type-2 Unique Rectangle", one of the blocks contains the floor squares, and the other contains the roof squares. In order to avoid the deadly pattern, 8 must appear in either R2C4 or R2C6 (the roof squares). Therefore, it can be removed from all other squares in the units (row, column and box) that contain both of the roof squares (in this case, row 2 and block 2). Now that you've gotten your head around the basic unique rectangle concept, the proof should be pretty obvious:
If neither R2C4 or R2C6 contains an 8, then they both become squares with possibilities 2/9. This results in the deadly pattern - so one of those squares must be the 8, and none of the other squares in the intersecting units can contain the 8. So R2C3, R3C4 and R3C6 can have 8 removed. This cracks the Sudoku.
Type 2B Unique Rectangles

There is a second variant of Type-2 Unique Rectangles as illustrated In Figure 4. In this puzzle, we have the same pattern of 4 squares in 2 blocks, 2 rows and 2 columns. The floor squares are R1C1 and R1C9, and the roof squares are R2C1 and R2C9. However, in this Unique Rectangle, each of the blocks contains one floor and one roof square. This is perfectly fine, but it means that the only unit (row/column/box) that contains both of the roof squares is row 2, so that is the only unit that you can attempt to reduce; in this case, R2C7 cannot contain a 8. This is called at "Type-2B Unique Rectangle".
Type 3 Unique Rectangles - Cracking the Rectangle with Conjugate Pairs
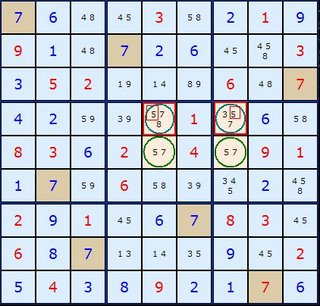
An interesting observation is that it is sometimes possible to remove one of the original pair of possibilities from the roof squares. Consider the following puzzle in Figure 5.
Look closely at the roof squares, R3C1 and R3C3, but this time, don't look at their extra possibilities; look at the possibilities they share with the floor squares. If you look carefully, you'll see that in box 1, the roof squares are the only squares that can contain a 5. This means that, no matter what, one of those squares must be 5 - and from this you can conclude that neither of the squares can contain a 1, since this would create the "deadly pattern"! So you can remove 1 from R3C1 and R3C3.
Nomenclature: When two squares are the only two squares in a unit that can have a particular value, they are referred to as a conjugate pair on that value.
This is an example of a "Type-3 Unique Rectangle". As you have probably realized, since the roof squares are in the same block, you can search for conjugate pairs in both of their common units (the row and the block, in this case).
Type 3B Unique Rectangles
And, as you might expect, there is a Type-3B Unique Rectangle variant, in which the floor squares are not in the same block, and you can only look for the conjugate pair in their common row or column. For example: In this case, since 7 can only appear in row 4 in the roof squares, 5 can be removed from both of them.
As Type-4 Unique Rectangle solutions "destroy" the Unique Rectangle, it is usually best to look for them only after you've done any other possible Unique Rectangle reductions.
Go To : Basic ||Fishy || Advanced
Go To : Sudoku solving techniques
No comments:
Post a Comment